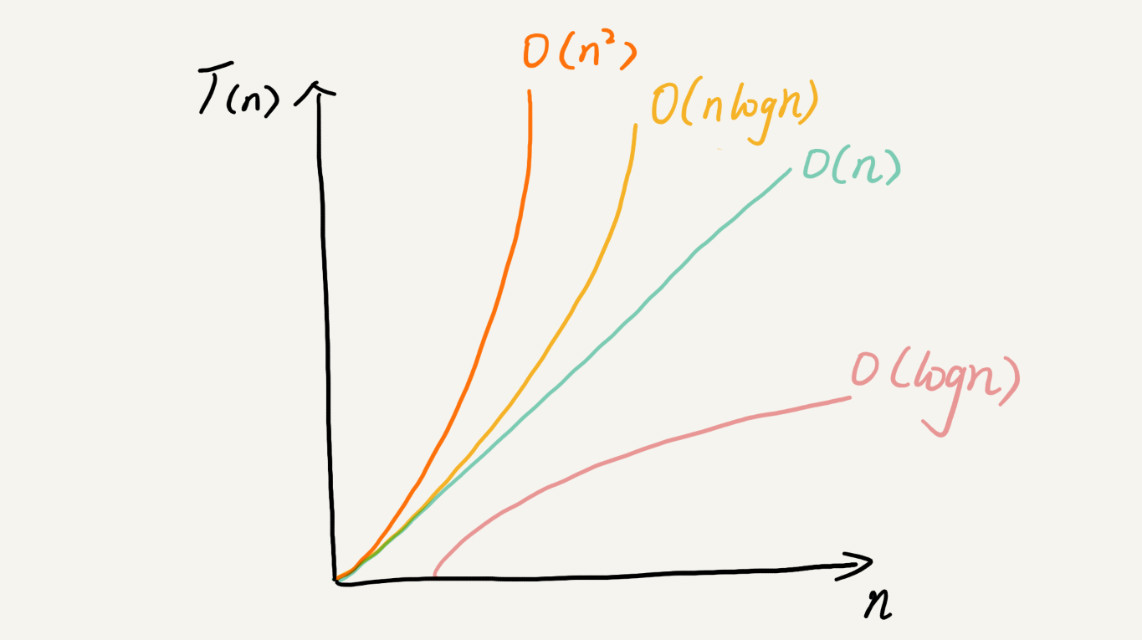
时间复杂度

- O(1)
1 | int i = 8; |
- O(logn)、O(nlogn)
1 | i=1; |
- O(m+n)、O(m*n)
代码的复杂度由两个数据的规模来决定,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m) * T2(n) = O(f(m) * f(n))。
空间复杂度
1 | void print(int n) { |
我们可以看到,第 2 行代码中,我们申请了一个空间存储变量 i,但是它是常量阶的,跟数据规模 n 没有关系,所以我们可以忽略。第 3 行申请了一个大小为 n 的 int 类型数组,除此之外,剩下的代码都没有占用更多的空间,所以整段代码的空间复杂度就是 O(n)。常见的空间复杂度就是 O(1)、O(n)、O(n2 )。
总结